Geometria Analítica - Posição Relativas entre 2 Retas
- Condição de Paralelismo de duas retas
- Duas retas r e s são paralelas quando têm direções iguais;
- Duas retas r e s são paralelas quando o coeficiente angular de um (Mr) for igual ao coeficiente angular da outra reta (Ms)
Veja a ilustração a seguir:
De acordo com a ilustração acima podemos analisar a seguinte condição:
Ou seja: Para que uma reta seja paralela o coeficiente angular de uma reta tem que ser igual ao coeficiente angular da outra reta, e os coeficientes lineares têm que ser diferentes.
Siga o exemplo abaixo:
Exemplo: Dentro de um plano, há duas retas. Uma reta r de equação x+y-2 = 0 e outra reta s de equação x+y-4 = 0. Qual a posição relativa entre essas duas retas?
Analisemos: Temos duas equações:
r: x+y-2 = 0
s: x+y-4 = 0
Devemos então REDUZIR ambas equações para que possamos retirar os coeficientes angular e linear. Vamos lá?
x + y - 2 = 0
y = -x + 2
Então temos que Mr = -1 e Nr = 2
x + y - 4 = 0
y = -x+4
Então temos que Ms = -1 e Nr = 4
Se eu tenho coeficientes angulares iguais e lineares diferentes, minha posição relativa entre essas duas retas será de PARALELISMO.
- Retas Coincidentes dentro do Plano
De acordo com a ilustração acima há duas retas; porém, ambas são coincidentes, o que nota-se aparentemente que é somente uma. E há uma "lei de formação" que possa ser feita para saber se é coincidente? Sim! Veja a seguir:
 Ou seja: Para que uma reta seja coincidente à outra, é necessário que os coeficientes angulares e os coeficientes lineares sejam todos iguais (por isso que anteriormente eu disse que era a mais fácil das retas, porque se tudo tá igual é porque a reta é concorrente). Ok? Siga o exemplo abaixo:
Ou seja: Para que uma reta seja coincidente à outra, é necessário que os coeficientes angulares e os coeficientes lineares sejam todos iguais (por isso que anteriormente eu disse que era a mais fácil das retas, porque se tudo tá igual é porque a reta é concorrente). Ok? Siga o exemplo abaixo:Exemplo: Em um plano cartesiano foi desenhado 2 retas. Uma chamada de reta w de equação 3x + y - 3 = 0 e outra chamada de reta z de equação 6x + 2y - 6 = 0. Determine a posição relativa entre essas duas retas.
Temos que:
w: 3x + y - 3 = 0
O que devemos fazer? Reduzir esta equação que está na forma geral...
3x + y - 3 = 0
y = -3x + 3
Então temos que: Mw = -3 e Nw = 3
z: 6x + 2y - 6 = 0
Reduzindo...
2y = -6x + 6
y = -6x + 6 y = -3x + 3
2
Então temos que Mz = -3 e Nz = 3
ANALISANDO: Mw é igual à Mz, e Nw é igual à Nz, o que nos leva a concluir que a posição relativa entre essas duas retas é de Coincidência.
- Retas Concorrentes - Perpendiculares e Não Perpendiculares
Sabemos na teoria matemática que, as retas concorrentes cruzam-se em um único ponto (a tão chamada: intersecção de duas retas), a partir dessa teoria tiramos nossas conclusões. Quais conclusões? Se são perpendiculares ou não perpendiculares.
Vamos trabalhar uma de cada vez.
Primeiro as concorrentes perpendiculares:
- A principal característica de uma reta perpendicular é: quando elas se cruzam elas formam um ângulo de 90º. Veja a ilustração a seguir:
De acordo com a ilustração acima podemos extrair dela informações:
- Ela é perpendicular, pois as retas que se interceptam no ponto P fazem um ângulo de 90º
- O ponto P é também chamado de ponto de perpendicularismo, ou melhor dizendo, ponto de intersecção das retas r e s
Existe uma nomenclatura bem simples para saber se as retas são ou não perpendiculares. Analise:
Ou seja: O Coeficiente Angular da Reta R multiplicado pelo Coeficiente Angular da Reta S tem necessariamente que resultar em -1. Veja o exemplo abaixo:
Exemplo: Qual a posição relativa de duas retas que possuem equações: x + y - 5 = 0 e -x + y = 0 , respectivamente?
Vamos calcular a primeira equação
x + y - 5 = 0
REDUZINDO...
y = -x + 5
Temos que: m = -1 e n = 5
-x + y = 0
REDUZINDO...
y = x
Temos que: m = 1 e n = 0
Agora, como saber se são perpendiculares? Lance os coeficientes angulares das duas retas na fórmula de perpendicularismo.
OBS: O Coeficiente Linear (n) não nos importa no perpendicularismo.
Mr . Ms = -1
(-1) . 1 = -1
Então conclui-se que essas retas são perpendiculares.
- Retas Não Perpendiculares
Pois bem... Retas não perpendiculares são apenas o contrário das características das perpendiculares, pois não fazem ângulos de 90º e os coeficientes angulares devem ser diferentes.
Analise a ilustração:
Note que mesmo estas retas tenham uma posição relativa não perpendicular, elas possuem uma característica do perpendicularismo: Ambos assuntos afirmam que as suas retas passam pelo ponto p, isto é, se interceptam neste ponto.
Veja o exemplo de ajuda abaixo:
Exemplo: Túlio desenhou numa malha quadriculada duas retas em um plano. Um professor de matemática analisou e chegou a conclusão de que as retas que Túlio desenhou tinham as respectivas equações: 2x + y - 6 = 0 e -2x + y + 1 = 0. A partir das equações, determine a posição relativa entre essas duas retas.
2x + y - 6 = 0
REDUZINDO...
y = -2x + 6 (m = -2 e n = 6)
-2x + y + 1 = 0
y = 2x - 1 (m = 2 e n = -1)
Note que os coeficientes angulares são diferentes, sendo assim essas retas são NÃO PERPENDICULARES.
OBS: Não é obrigatório olhar o valor do coeficiente linear, pois ele não nos importa no estudo de retas perpendiculares e não perpendiculares.

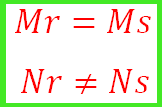





Comentários
Postar um comentário