Atividades de Geometria Analítica - Retas
Atividades - Geometria Analítica - Retas
1) Duas retas de equações: y = 3x + 1 e -3x + y - 1 = 0 foram desenhadas em uma folha de caderno de um aluno de 3ºAno. Determine a posição relativa entre essas retas.
2) Em um Plano Cartesiano, foi esboçada duas retas r e s. A reta r passa pelos pontos A(2,3) e B(6,2) e a reta s passa pelos pontos K(-1,0) e W(2,-1).
a) Determine os coeficientes angulares e lineares de ambas as retas.
b) Determine o ponto médio das retas r e s.
c) Determine a distância entre os pontos da reta r
d) Determine a distância entre os pontos da reta s
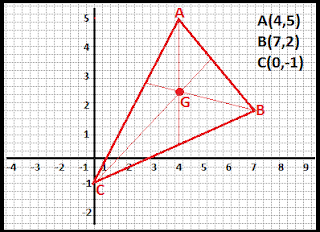
3) Antônio esboçou um triângulo numa malha quadriculada como na ilustração abaixo:
Com base neste triângulo, o Ponto G, a Área deste triângulo e o quadrante em que o baricentro está localizado, são respectivamente...
a) G(11/3, 2) , 30u.a, 2º quadrante
b) G(2, 11/3) , 15u.a, 2º quadrante
c) G(11/3, 2) , 15u.a, 1º quadrante
d) G(11/3, 2) , 30u.a, 1º quadrante
4) O gráfico abaixo apresenta o comportamento de um resistor.
Determine os coeficientes angular e linear das duas retas.
(OBS: Desconsidere a origem)
5) Qual a medida de um segmento de reta com extremidades nos pontos P(8,0) e Q(0,6)?
6) O que se pode afirmar da reta abaixo?
a) É colinear.
b) Possui coeficiente angular 0 e linear 2
c) Passa pelos pontos (-2,0) e (0,2) que fazem parte do 1º e 3º quadrantes respectivamente.
d) Possui coeficiente linear 2
e) Sua equação geral é x= y+2
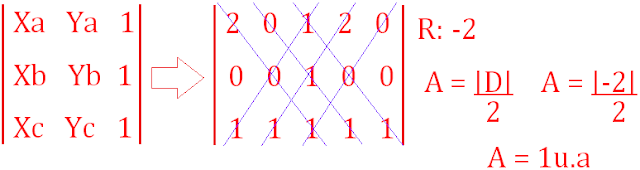
7) Considere um triângulo que passa pelos pontos A(2,0) B(0,0) e C(1,1). Qual a área desse triângulo em u.a?
8) Analise as equações abaixo:
I. 2x+y-3 = 0
II. x+y = 0
III. y = x
IV. y²=x²+5
V. y = 2x+10
Qual das equações acima são equações reduzidas da reta?
a) I e II b) I e IV c) II e III d) III e IV e) III e V
9) Se uma bissetriz passa pela origem e atinge os pontos (3,3) e (-1,-3), então essa bissetriz pertence...
a) Aos quadrantes ímpares;
b) Aos quadrantes pares;
c) A nenhum quadrante;
d) aos colineares.
10) Determine a área de um triângulo cujas extremidades passam nos pontos A(origem) B(5,-3) C (10, 1/2).
a)63u.a
b)64u.a
c)65u.a
d)66u.a
e)67u.a
Ou seja, o ponto médio da reta r é M(4, 5/2).
Ok. Agora que sabemos o ponto médio da reta r, vamos descobrir o ponto médio da reta s.
Xa + Xb = -1 + 2 = 1 u.c
2 2 2
Ya + Yb = 0 - 1 = -1 u.c
2 2 2
Ou seja, o ponto médio da reta s é M(1/2 , -1/2)
Bem simples né?!
c e d) Determinar a distância entre os pontos. Para isso precisaremos das 4 coordenadas para fazermos 2 contas, igual ao exercício anterior. Veja:
3) Devemos analisar todos os pontos que o exercício deu na imagem. Primeiramente iremos calcular o Ponto G (Baricentro)
Xa + Xb + Xc = 4+7+0 = 11u.c
3 3 3
Ya + Yb + Yc = 5+2+(-1) = 7-1 = 6 = 2u.c
3 3 3 3
Então descobrimos que as coordenadas do Ponto G é G(11/3 , 2)
Vamos agora calcular a área.
Então descobrimos também que a área deste triângulo é 15u.a.
E como contamos os quadrantes em sentido anti-horário, o quadrante em que se localiza o Ponto G é o 1º quadrante.
4) Primeiramente, faremos o determinante com os pontos da reta R...
Agora vamos fazer o determinante com os pontos da reta S...
OBS: Chegamos então nas respostas dos coeficientes que estão nas chaves acima.
5) Temos que ter em mente que quando se fala de MEDIDA (na Geometria Analítica) ele quer saber a quantidade, isto é, a unidade de comprimento da reta (u.c).E só conseguimos achá-la por meio da fórmula da distância entre 2 pontos. Veja:
A seta roxa aponta que o coeficiente linear é 2, então a alternativa que aponta que o coeficiente linear é 2, é a Letra D.
7) Para descobrirmos uma área de um triângulo analítico, devemos usar o módulo do determinante dividido por 2. Veja:
8) Vamos analisar uma a uma.
- A primeira não é reduzida, é geral.
- A segunda também é uma equação geral.
-A terceira é uma equação reduzida da reta, pois tem a incógnita "y" isolada no primeiro membro (Alternativa verdadeira)
- A quarta não é reduzida pois tem termos elevados ao quadrado
- A quinta com certeza é uma equação reduzida, pois também apresenta a variável "y" isolada no primeiro membro.
ALTERNATIVAS VERDADEIRAS: III e V (Letra E)
9) Podemos resolvê-lo pela lógica, mas vamos esboçar para obter mais clareza do fundamento da resposta...
Note que a bissetriz foi desenhada do mesmo jeito supracitado no enunciado. Os números romanos estão assumindo o papel do quadrante respectivo, ou seja, o ponto (3,3) pertence ao quadrante 1, o ponto (-1,-3) pertence ao quadrante 3. Como 1 e 3 são ímpares, então essa é uma bissetriz dos quadrantes ímpares.
ALTERNATIVA CORRETA: Letra A
10) Vamos lançar os pontos no determinante e logo em seguida aplicar a fórmula da Área Triangular...
Resposta Final: Letra C.
3) Antônio esboçou um triângulo numa malha quadriculada como na ilustração abaixo:
Com base neste triângulo, o Ponto G, a Área deste triângulo e o quadrante em que o baricentro está localizado, são respectivamente...
a) G(11/3, 2) , 30u.a, 2º quadrante
b) G(2, 11/3) , 15u.a, 2º quadrante
c) G(11/3, 2) , 15u.a, 1º quadrante
d) G(11/3, 2) , 30u.a, 1º quadrante
4) O gráfico abaixo apresenta o comportamento de um resistor.
(OBS: Desconsidere a origem)
5) Qual a medida de um segmento de reta com extremidades nos pontos P(8,0) e Q(0,6)?
6) O que se pode afirmar da reta abaixo?
a) É colinear.
b) Possui coeficiente angular 0 e linear 2
c) Passa pelos pontos (-2,0) e (0,2) que fazem parte do 1º e 3º quadrantes respectivamente.
d) Possui coeficiente linear 2
e) Sua equação geral é x= y+2
7) Considere um triângulo que passa pelos pontos A(2,0) B(0,0) e C(1,1). Qual a área desse triângulo em u.a?
8) Analise as equações abaixo:
I. 2x+y-3 = 0
II. x+y = 0
III. y = x
IV. y²=x²+5
V. y = 2x+10
Qual das equações acima são equações reduzidas da reta?
a) I e II b) I e IV c) II e III d) III e IV e) III e V
9) Se uma bissetriz passa pela origem e atinge os pontos (3,3) e (-1,-3), então essa bissetriz pertence...
a) Aos quadrantes ímpares;
b) Aos quadrantes pares;
c) A nenhum quadrante;
d) aos colineares.
10) Determine a área de um triângulo cujas extremidades passam nos pontos A(origem) B(5,-3) C (10, 1/2).
a)63u.a
b)64u.a
c)65u.a
d)66u.a
e)67u.a
Respostas
1) Temos que:
y = 3x + 1 e -3x + y - 1 = 0
Para determinar posição relativa devemos retirar os coeficientes angulares das retas. OBS: Note que a 2ª equação está na forma GERAL então deve-se REDUZIR ela. Mas vamos passo a passo:
Equação 1: m = 3 e n = 1
Equação 2: -3x + y - 1 = 0
y = 3x + 1 ---> m = 3 e n = 1
Chegamos então a conclusão de que a única espécie de reta que possui coeficientes angulares e lineares iguais, é reta coincidente.
Então, são RETAS COINCIDENTES
2)
a)
Achamos os coeficientes angular e linear da reta r, faremos agora os coeficientes da reta s...
Temos então os coeficientes da reta s, como mostra o círculo acima.
b) Calculando o ponto médio da reta r
Xa + Xb = 2 + 6 = 8 = 4u.c
2 2 2
Ya + Yb = 3 + 2 = 5 u.c
2 2 2Xa + Xb = 2 + 6 = 8 = 4u.c
2 2 2
Ya + Yb = 3 + 2 = 5 u.c
Ou seja, o ponto médio da reta r é M(4, 5/2).
Ok. Agora que sabemos o ponto médio da reta r, vamos descobrir o ponto médio da reta s.
Xa + Xb = -1 + 2 = 1 u.c
2 2 2
Ya + Yb = 0 - 1 = -1 u.c
2 2 2
Ou seja, o ponto médio da reta s é M(1/2 , -1/2)
Bem simples né?!
c e d) Determinar a distância entre os pontos. Para isso precisaremos das 4 coordenadas para fazermos 2 contas, igual ao exercício anterior. Veja:
3) Devemos analisar todos os pontos que o exercício deu na imagem. Primeiramente iremos calcular o Ponto G (Baricentro)
Xa + Xb + Xc = 4+7+0 = 11u.c
3 3 3
Ya + Yb + Yc = 5+2+(-1) = 7-1 = 6 = 2u.c
3 3 3 3
Então descobrimos que as coordenadas do Ponto G é G(11/3 , 2)
Vamos agora calcular a área.
Então descobrimos também que a área deste triângulo é 15u.a.
E como contamos os quadrantes em sentido anti-horário, o quadrante em que se localiza o Ponto G é o 1º quadrante.
4) Primeiramente, faremos o determinante com os pontos da reta R...
Agora vamos fazer o determinante com os pontos da reta S...
OBS: Chegamos então nas respostas dos coeficientes que estão nas chaves acima.
5) Temos que ter em mente que quando se fala de MEDIDA (na Geometria Analítica) ele quer saber a quantidade, isto é, a unidade de comprimento da reta (u.c).E só conseguimos achá-la por meio da fórmula da distância entre 2 pontos. Veja:
6) Logo de cara analisamos que não pode ser colinear (pois precisaria de 3 pontos numa única reta). Então descartamos a Letra A. Quando os pontos estão em cima do plano, elas não pertencem à NENHUM quadrante, então a Letra C também está errada. Agora precisamos fazer um determinante para descobrir a equação geral e reduzida desta reta.
7) Para descobrirmos uma área de um triângulo analítico, devemos usar o módulo do determinante dividido por 2. Veja:
8) Vamos analisar uma a uma.
- A primeira não é reduzida, é geral.
- A segunda também é uma equação geral.
-A terceira é uma equação reduzida da reta, pois tem a incógnita "y" isolada no primeiro membro (Alternativa verdadeira)
- A quarta não é reduzida pois tem termos elevados ao quadrado
- A quinta com certeza é uma equação reduzida, pois também apresenta a variável "y" isolada no primeiro membro.
ALTERNATIVAS VERDADEIRAS: III e V (Letra E)
9) Podemos resolvê-lo pela lógica, mas vamos esboçar para obter mais clareza do fundamento da resposta...
Note que a bissetriz foi desenhada do mesmo jeito supracitado no enunciado. Os números romanos estão assumindo o papel do quadrante respectivo, ou seja, o ponto (3,3) pertence ao quadrante 1, o ponto (-1,-3) pertence ao quadrante 3. Como 1 e 3 são ímpares, então essa é uma bissetriz dos quadrantes ímpares.
ALTERNATIVA CORRETA: Letra A
10) Vamos lançar os pontos no determinante e logo em seguida aplicar a fórmula da Área Triangular...
Resposta Final: Letra C.
"A matemática não mente, mente quem faz mal uso dela"
Albert Einstein
OBRIGADO!!












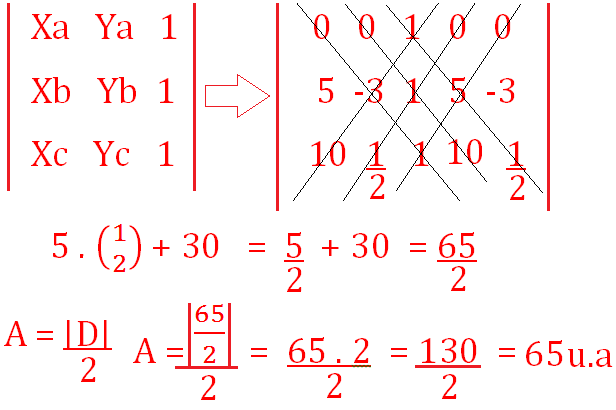


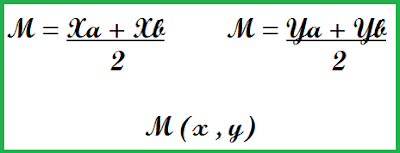
Find the best Casino Bonuses | DrmCD
ResponderExcluirA full list 천안 출장마사지 of all bonuses and promotions available to all Casino players, 경상남도 출장샵 sorted by bonuses and games. The best bonuses 김제 출장마사지 and 김제 출장마사지 bonuses at the best Casino 김제 출장마사지 Bonuses.