Geometria Analítica - Equação Geral da Reta
Equação Geral da Reta
- Condição de Alinhamento de 3 pontos
OBS: Em um determinante 3x3, pegamos as 2 primeiras colunas e lançamos ela para a direita. Veja o exemplo abaixo:
Exemplo: Verifique se os pontos A(3,2), B(4,1) e C(1,4) estão alinhados.
Primeiramente: fazer o determinante
Seguidamente: deve-se ter em mente que seu determinante dele valer 0 (zero) para seus pontos serem alinhados.
Com base nisso, concluímos que os pontos mencionados no exercício são sim alinhados. Por que? Porque o resultado do Determinante Geral deu 0 (zero), o que também significa que estes pontos pertencem à mesma reta!
- Equação Geral da Reta
Vimos anteriormente que através do determinante tem como descobrir se os pontos estão ou não alinhados. Não abandonaremos o determinante, usaremos ele para descobrir as equações de uma reta. A equação geral da reta é dada por:
Onde:
a = Número que acompanha x
b = Número que acompanha y
c = termo independente
OBS: sempre que quisermos calcular equação geral devemos igualar nosso determinante a zero.
Como usar o Determinante para descobrir a equação de uma reta? Veja a seguir:
Com um exemplo, a compreensão do assunto ficará melhor. Veja:
Exemplo: Qual a equação geral de uma reta que passa pelos pontos A(2,1) e B(3,0)?
Primeiramente: Lançar no determinante dado acima.
Concluímos a partir daí que a equação geral desta reta é X+Y-3 = 0
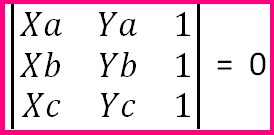






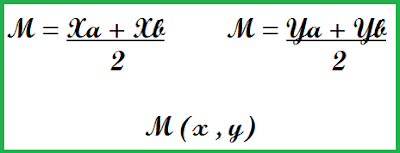
Comentários
Postar um comentário