Geometria Analítica - RETAS

Geometria Analítica - Retas

  • Ponto Médio de uma reta (P.M.)
Como o próprio nome já diz, o ponto médio é o ponto que se encontra no meio de dois pontos de uma reta no plano cartesiano.
E existe uma nomenclatura própria e bem fácil para calcular o ponto médio de uma reta. Veja:
Como podemos ver acima, é necessário visualizar os pares ordenados dos 2 pontos para se saber o valor de x de ambos e o valor de y de ambos (que é necessário para calcular o ponto médio).

Exemplo: Uma reta passa pelos pontos A(3,3) e B(3,11) no Plano Cartesiano. Determine o ponto médio dessa reta.
M = Xa + Xb      M = 3 + 3      M =  6    M = 3
              2                       2                  2
- Note que a operação gira em torno dos pares ordenados, neste caso achamos uma parte do ponto médio, pois sabemos que o ponto médio dessa reta tem abscissa (x) igual a 3. - M(3,y). Agora vamos achar y.

M = Ya + Yb     M = 3 + 11      M = 14      M = 7
              2                      2                   2         
- Perfeito! Achamos nosso par ordenado do Ponto Médio, ou seja, o meu Ponto Médio tem coordenadas (3,7).

OBS: Se colocarmos (7,3) fica errado?? SIM!! SUPER ERRADO!! Pois sempre se usa o valor de X primeiro para depois o valor de Y. Sempre será assim, enquanto estudarmos Geometria Analítica.

  • Distância entre 2 pontos (Dab)
Sabemos até aqui que existe um ponto médio no meio de dois pontos, que é necessário visualizar um par ordenado e que toda conta circula em volta de suas coordenadas. Pois bem... Veremos agora que é possível calcular a distância de um ponto até o outro, sendo que esses 2 pontos estão em cima de uma reta.

OBSERVAÇÃO:
  • Significado Simbológico - Dab = Distância entre o ponto A e o ponto B (dentro do plano cartesiano)
 Nomenclatura da Distância entre Dois Pontos



Exemplo: Considere uma reta que passa pela ORIGEM do plano cartesiano e pelo ponto B(3,0). Determine a distância entre esses pontos.
Primeiramente... O QUE É ORIGEM? Origem é o ponto (0,0) do plano cartesiano, também conhecido como ponto de intersecção dos eixos: abscissa e ordenada. (Lembrando que abscissa é x, e ordenada é y). Bom... Agora vamos calcular:




OBS: "u.c" significa unidade(s) de comprimento.



Então chegamos a conclusão de que a distância entre a orgiem e o ponto B é de 3u.c.

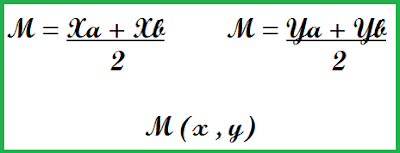
Comentários

Postar um comentário

Postagens mais visitadas deste blog

Geometria Analítica - Baricentro

Imagem
Baricentro de um Triângulo (Ponto G) O Baricentro é o ponto central de um triângulo representado num plano cartesiano. Logicamente é necessário que se tenha 3 pontos (A,B e C) para se calcular baricentro.  Note que na exemplificação acima há 3 coordenadas (fundamentais) e o círculo azul claro simboliza o baricentro. O Baricentro é chamado também de PONTO G. Soa engraçado (hehehe) mas é verdade. Então, não se esqueçam, se o exercício pediu para determinar o baricentro, ele quer que você ache apenas o ponto G. E como calcular o Ponto G? Existe fórmula específica para ele? Sim! Existe! A fórmula é bem simples. Veja a seguir: Complemento: Você irá apenas precisar dos valores de x e y e dividi-los por 3. Por que por 3? Porque um triângulo possui 3 lados. Ok? Veja o exemplo abaixo: Exemplo: Determine o Baricentro (Ponto G) de um triângulo cujos vértices possuem os respectivos pares ordenados: A(6,2), B(2,4) e C(4,-2). Calculando X:                           Calculando Y:
Leia mais

Atividades de Geometria Analítica - Retas

Imagem
Atividades - Geometria Analítica - Retas 1) Duas retas de equações: y = 3x + 1 e -3x + y - 1 = 0 foram desenhadas em uma folha de caderno de um aluno de 3ºAno. Determine a posição relativa entre essas retas. 2) Em um Plano Cartesiano, foi esboçada duas retas r e s. A reta r passa pelos pontos A(2,3) e B(6,2) e a reta s passa pelos pontos K(-1,0) e W(2,-1). a) Determine os coeficientes angulares e lineares de ambas as retas. b) Determine o ponto médio das retas r e s. c) Determine a distância entre os pontos da reta r d) Determine a distância entre os pontos da reta s 3) Antônio esboçou um triângulo numa malha quadriculada como na ilustração abaixo: Com base neste triângulo, o Ponto G, a Área deste triângulo e o quadrante em que o baricentro está localizado, são respectivamente... a) G(11/3, 2) , 30u.a, 2º quadrante b) G(2, 11/3) , 15u.a, 2º quadrante c) G(11/3, 2) , 15u.a, 1º quadrante d) G(11/3, 2) , 30u.a, 1º quadrante 4) O gráfico abaixo apresenta o co
Leia mais

Geometria Analítica - Posição Relativas entre 2 Retas

Imagem
Condição de Paralelismo de duas retas Existem vários elementos que comprovam o paralelismo entre 2 retas em um plano, dentre os quais cabe citar: - Duas retas r e s  são paralelas quando têm direções iguais; - Duas retas r e s são paralelas quando o coeficiente angular de um ( Mr ) for igual ao coeficiente angular da outra reta ( Ms ) Veja a ilustração a seguir: De acordo com a ilustração acima podemos analisar a seguinte condição: Ou seja: Para que uma reta seja paralela o coeficiente angular de uma reta tem que ser igual ao coeficiente angular da outra reta, e os coeficientes lineares têm que ser diferentes. Siga o exemplo abaixo: Exemplo: Dentro de um plano, há duas retas. Uma reta r de equação x+y-2 = 0 e outra reta s de equação x+y-4 = 0. Qual a posição relativa entre essas duas retas? Analisemos: Temos duas equações: r: x+y-2 = 0 s: x+y-4 = 0 Devemos então REDUZIR ambas equações para que possamos retirar os coeficientes angular e linear. Vamos lá? x +
Leia mais