ATIVIDADES DE GEOMETRIA PLANA
Atividades - Geometria Plana
1) Considere um triângulo equilátero com 23 cm de altura relativa e sua base é 25 cm. Encontre valor da área deste triângulo.
2) Analise as proposições e assinale a(s) alternativa(s) FALSA(S):
I. O Triângulo Equilátero possui todos os lados de mesma medida
II. A partir de um Triângulo Isósceles, foi desenvolvida (dentro da matemática) uma disciplina chamada Relações Métricas.
III. Somente se calcula o Perímetro de um Triângulo Equilátero obtendo-se o resultado entre o produto da base + altura divida por 2.
A proposição falsa é...
a) I b) II c) III d) II e III e) I e II
3) Qual o valor da área de um trapézio cujas bases assumem valores de 6m e 3m e sua altura é 5m?
5) Traçando-se uma diagonal d sobre um retângulo e desmembrando-o a partir desta diagonal, obtemos dois triângulos como na ilustração abaixo
Suponha que T1 tenha 20cm² de área e 4 cm de base, e que
T2 tenha 2√3 cm de base e √3 cm de altura.
Com base nos dados acima, a altura de T1, a área de T2 e a área do retângulo que sofreu a extração será...
a) 20cm, 13cm², 23cm²
b) 10cm, 3cm², 13cm²
c) 10cm, 3cm², 23cm²
d) Nenhuma das Anteriores
Respostas
A = B.h A = 25.23 A = 575 A = 287,5 cm²
2 2 2
OBS: Não se esqueçam de elevar a unidade ao quadrado quando o exercício pedir ÁREA.
2) O triângulo equilátero possui todos os lados de mesma medida, então a proposição I está correta;
As relações métricas no triângulo foi uma matéria desenvolvida a partir de estudos sobre os triângulos sim, porém, não com o triângulo isósceles, então a proposição II está incorreta;
Não calcula-se o perímetro de um triângulo com base + altura dividida por 2 e nem tampouco a área (pois a área triangular é base . altura /2), portanto a proposição III também está incorreta.
ALTERNATIVA D (II e III)
3) Sabemos que a nomenclatura para área do trapézio é:
A = (B+b).h A = (6+3).5 A = 9.5 A = 45 = 22,5 cm²
2 2 2 2
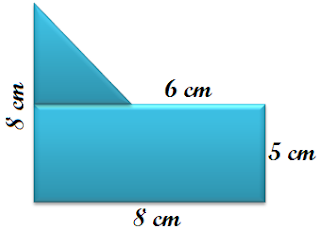
4) Conseguimos analisar a partir desta figura que ela é formada por um retângulo e por um triângulo. Iremos fazer uso da fórmula de cada um... Primeiro do Retângulo:
A = b.h
A = 8.5 = 40 cm²
Agora que sabemos a área do retângulo, nos resta saber a área do triângulo.
Analisemos...
Se a base inferior (do retângulo) é 8cm, e a base superior (do retângulo) é 6cm, então a base do triângulo será 8cm - 6cm = 2cm.
Agora nos resta descobrir a altura, analisemos novamente:
Se a altura relativa (que pega o triângulo e o retângulo juntos) é 8cm, e a altura do retângulo é 5cm, temos que 8cm - 5cm = 3cm
Note então que temos: B = 2cm e h = 3cm, vamos descobrir a área:
A = B.h A = 2.3 A = 6 A = 3cm²
2 2 2
Só falta uma coisa: A área total da figura: 40+3 = 43cm²
5) Temos que T1 tem A = 20cm² e B = 4cm. Vamos achar a altura:
A = B.h 20 = 4h 4h = 20.2 4h = 40 h = 40 h = 10cm
2 2 4
Temos que T2 tem B = 2√3 cm e h = √3 cm
A = 2√3 . √3 A = 2√9 A = 2.3 A = 6 A = 3cm²
2 2 2 2
ÁREA DO TRIÂNGULO 1 = 20
ÁREA DO TRIÂNGULO 2 = 3
Se juntarmos os triângulos do mesmo jeito que ele foi extraído ele virará um retângulo, e para saber sua área é só somar a área dos triângulos (T1 e T2) = 20cm² + 3cm² = 23cm²
RESPOSTA: Letra C




Comentários
Postar um comentário