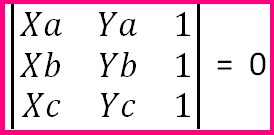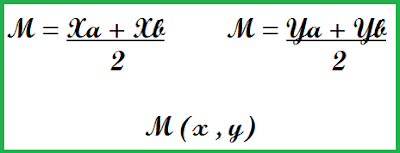Postagens

Atividades de Geometria Analítica - Retas

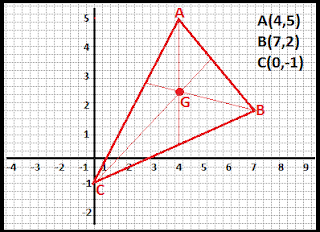
Imagem
Atividades - Geometria Analítica - Retas 1) Duas retas de equações: y = 3x + 1 e -3x + y - 1 = 0 foram desenhadas em uma folha de caderno de um aluno de 3ºAno. Determine a posição relativa entre essas retas. 2) Em um Plano Cartesiano, foi esboçada duas retas r e s. A reta r passa pelos pontos A(2,3) e B(6,2) e a reta s passa pelos pontos K(-1,0) e W(2,-1). a) Determine os coeficientes angulares e lineares de ambas as retas. b) Determine o ponto médio das retas r e s. c) Determine a distância entre os pontos da reta r d) Determine a distância entre os pontos da reta s 3) Antônio esboçou um triângulo numa malha quadriculada como na ilustração abaixo: Com base neste triângulo, o Ponto G, a Área deste triângulo e o quadrante em que o baricentro está localizado, são respectivamente... a) G(11/3, 2) , 30u.a, 2º quadrante b) G(2, 11/3) , 15u.a, 2º quadrante c) G(11/3, 2) , 15u.a, 1º quadrante d) G(11/3, 2) , 30u.a, 1º quadrante 4) O gráfico abaixo apresenta o co
1 comentário
Leia mais

Geometria Analítica - Área Triângular

Imagem
Área do Triângulo (Geometria Analítica) Aprendemos na GEOMETRIA PLANA que a área de um triângulo é base x altura dividida por 2 . Iremos a partir daqui, estudar uma ramificação totalmente distinta, pois o triângulo que é estudado na Geometria Plana não é o mesmo estudo na GEOMETRIA ANALÍTICA.  O Triângulo em si possui 3 retas dentro do plano, e automaticamente, possui coordenadas em cada vértice (o que também nos leva a confirmar que ele tem coeficientes m e n, e que ele tem equações reduzidas e gerais). Mas ao invés de calcular reta a reta, os matemáticos da época fizeram uso do mecanismo mais utilizado dentro de cálculos analíticos, o determinante. Ou seja, é possível saber a área de um triângulo através de um determinante. Veja a seguir: Onde: Xa e Ya = Coordenadas do Ponto A Xb e Yb = Coordenadas do Ponto B Xc e Yc = Coordenadas do Ponto C D = Determinante Geral  |   |   = Módulos R = Qualquer número real Detalhe: Para que serve o módulo? O Módulo serve
Postar um comentário
Leia mais

Geometria Analítica - Posição Relativas entre 2 Retas

Imagem
Condição de Paralelismo de duas retas Existem vários elementos que comprovam o paralelismo entre 2 retas em um plano, dentre os quais cabe citar: - Duas retas r e s  são paralelas quando têm direções iguais; - Duas retas r e s são paralelas quando o coeficiente angular de um ( Mr ) for igual ao coeficiente angular da outra reta ( Ms ) Veja a ilustração a seguir: De acordo com a ilustração acima podemos analisar a seguinte condição: Ou seja: Para que uma reta seja paralela o coeficiente angular de uma reta tem que ser igual ao coeficiente angular da outra reta, e os coeficientes lineares têm que ser diferentes. Siga o exemplo abaixo: Exemplo: Dentro de um plano, há duas retas. Uma reta r de equação x+y-2 = 0 e outra reta s de equação x+y-4 = 0. Qual a posição relativa entre essas duas retas? Analisemos: Temos duas equações: r: x+y-2 = 0 s: x+y-4 = 0 Devemos então REDUZIR ambas equações para que possamos retirar os coeficientes angular e linear. Vamos lá? x +
Postar um comentário
Leia mais

Geometria Analítica - Continuação do Estudo de Retas

Imagem
Equação Reduzida da Reta Já vimos anteriormente que a equação geral da reta é dada pela formação ax+by+c = 0 . A equação reduzida da reta não é nada mais que a derivação de uma geral. O que é isso? Isolamento da variável "y". E (da mesma forma) usaremos novamente o determinante para achar a equação reduzida.  A nomenclatura geral para uma equação reduzida da reta é: Então temos que: m = coeficiente angular    n = coeficiente linear OBS: Note que a fórmula da equação reduzida se assemelha à da função do 1º grau ( f(x) = ax+b ). Isso porque as retas nos estudos de função do 1º grau são utilizadas também na Geometria Analítica. Qual a diferença então? A diferença é que, na função afim as retas que são estudadas não precisam de uma equação para suas retas (nem geral e nem reduzida), já a Geometria Analítica, abrange toda matéria de função do 1º grau e através desses estudos conjectura-se uma equação reduzida e/ou geral de uma determinada reta. Analise o exem
Postar um comentário
Leia mais

Geometria Analítica - Equação Geral da Reta

Imagem
Equação Geral da Reta Condição de Alinhamento de 3 pontos Devemos ter em mente de que, por dois pontos distintos passa uma única reta, portanto eles estão sempre alinhados. Partindo disso, existe uma maneira de se descobrir se 3 pontos (que pertencem a mesma reta) são alinhados. A maneira mais usada atualmente é: fazer um determinante dos pontos que você tiver na sua reta, e se o resultado for zero então seus pontos estão alinhados. OBS: Em um determinante 3x3, pegamos as 2 primeiras colunas e lançamos ela para a direita. Veja o exemplo abaixo: Exemplo: Verifique se os pontos A(3,2), B(4,1) e C(1,4) estão alinhados. Primeiramente: fazer o determinante Seguidamente: deve-se ter em mente que seu determinante dele valer 0 (zero) para seus pontos serem alinhados. Com base nisso, concluímos que os pontos mencionados no exercício são sim alinhados. Por que? Porque o resultado do Determinante Geral deu 0 (zero), o que também significa que estes pontos perte
Postar um comentário
Leia mais

Geometria Analítica - Baricentro

Imagem
Baricentro de um Triângulo (Ponto G) O Baricentro é o ponto central de um triângulo representado num plano cartesiano. Logicamente é necessário que se tenha 3 pontos (A,B e C) para se calcular baricentro.  Note que na exemplificação acima há 3 coordenadas (fundamentais) e o círculo azul claro simboliza o baricentro. O Baricentro é chamado também de PONTO G. Soa engraçado (hehehe) mas é verdade. Então, não se esqueçam, se o exercício pediu para determinar o baricentro, ele quer que você ache apenas o ponto G. E como calcular o Ponto G? Existe fórmula específica para ele? Sim! Existe! A fórmula é bem simples. Veja a seguir: Complemento: Você irá apenas precisar dos valores de x e y e dividi-los por 3. Por que por 3? Porque um triângulo possui 3 lados. Ok? Veja o exemplo abaixo: Exemplo: Determine o Baricentro (Ponto G) de um triângulo cujos vértices possuem os respectivos pares ordenados: A(6,2), B(2,4) e C(4,-2). Calculando X:                           Calculando Y:
1 comentário
Leia mais

Geometria Analítica - RETAS

Imagem
Geometria Analítica - Retas Ponto Médio de uma reta (P.M.) Como o próprio nome já diz, o ponto médio é o ponto que se encontra no meio de dois pontos de uma reta no plano cartesiano. E existe uma nomenclatura própria e bem fácil para calcular o ponto médio de uma reta. Veja: Como podemos ver acima, é necessário visualizar os pares ordenados dos 2 pontos para se saber o valor de x de ambos e o valor de y de ambos (que é necessário para calcular o ponto médio). Exemplo: Uma reta passa pelos pontos A(3,3) e B(3,11) no Plano Cartesiano. Determine o ponto médio dessa reta. M = Xa + Xb       M = 3 + 3       M =  6    M = 3               2                       2                  2 - Note que a operação gira em torno dos pares ordenados, neste caso achamos uma parte do ponto médio, pois sabemos que o ponto médio dessa reta tem abscissa (x) igual a 3. - M(3,y). Agora vamos achar y. M = Ya + Yb     M = 3 + 11      M = 14      M = 7               2              
Postar um comentário
Leia mais